Bạn đã bao giờ tự hỏi về cách tính diện tích hình tam giác chưa? Diện tích hình tam giác là một khái niệm toán học quan trọng. Trong bài viết này, oshovietnam.org sẽ chia sẻ những kiến thức tổng hợp để bạn hiểu rõ hơn về cách tính diện tích của hình tam giác.
Định nghĩa về tam giác là gì?
Tam giác, hay hình tam giác, là một dạng hình cơ bản trong hình học, thuộc hình hai chiều phẳng, có ba đỉnh không thẳng hàng. Và ba cạnh là ba đoạn thẳng nối các đỉnh với nhau. Tam giác là một đa giác có ít nhất ba cạnh và chỉ có ba góc.
Bạn đang xem: Diện Tích Hình Tam Giác – Một Khái Niệm Quan Trọng Trong Toán Học
Tam giác luôn là một đa giác đơn và luôn là một đa giác lồi, tức là các góc trong tam giác luôn nhỏ hơn 180 độ. Một tam giác có các cạnh AB, BC và AC được gọi là tam giác ABC.
Các góc trong tam giác được gọi là góc trong. Các góc ngoài là các góc kề bù với góc trong. Góc ngoài bằng tổng các góc trong không kề bù với nó. Mỗi tam giác chỉ có ba góc trong và sáu góc ngoài.
Các loại tam giác thường gặp
Khi nói về hình học, chắc hẳn ai cũng có khái niệm về việc so sánh, phân biệt các hình dạng, đoạn thẳng và các góc trong tam giác. Có thể phân loại tam giác theo hai yếu tố khác nhau. Một tam giác có thể được đặt tên theo các góc hoặc cạnh của hình, hoặc cả hai yếu tố này.
Phân loại tam giác theo cạnh, ta có thể dùng thước để đo ba cạnh của tam giác, đặt thước dọc theo một cạnh và đo từ đầu cạnh đó đến điểm giao nhau với cạnh đối diện. Sau đó, ghi lại độ dài mỗi cạnh, so sánh chiều dài các cạnh với nhau, từ đó có thể kiểm tra xem cạnh nào dài hơn hoặc các cạnh có bằng nhau.
Tam giác thường
Tam giác thường là tam giác đơn giản nhất, có các cạnh có độ dài khác nhau và các góc trong cũng khác nhau.
Tam giác cân
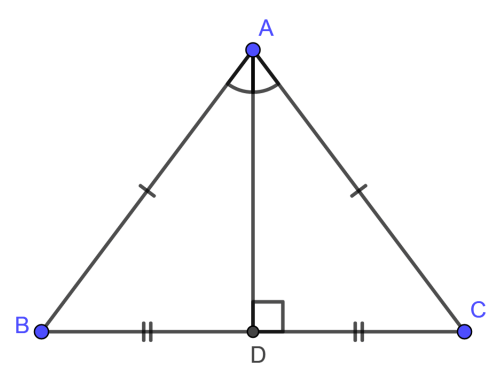
Tam giác cân là tam giác có hai cạnh bằng nhau, cạnh này được gọi là cạnh bên. Đỉnh của một tam giác cân là giao điểm của hai cạnh bên. Góc tạo bởi đỉnh được gọi là góc ở đỉnh, hai góc còn lại được gọi là góc ở đáy. Tính chất của tam giác cân là hai góc ở đáy bằng nhau.
Tam giác cân
Tam giác đều
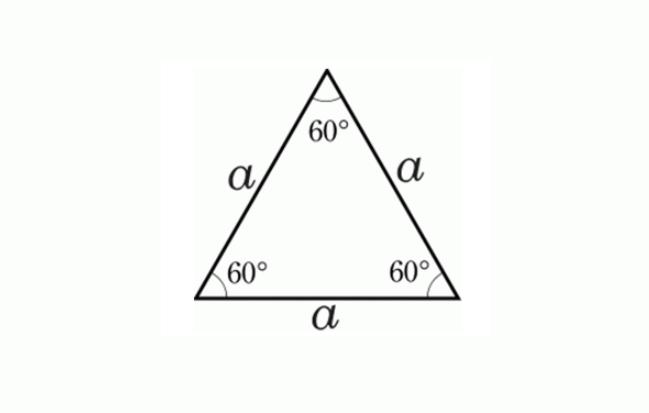
Tam giác đều là trường hợp đặc biệt của tam giác cân, có cả ba cạnh bằng nhau. Tính chất của tam giác đều là có ba góc bằng nhau và bằng 60 độ.
Xem thêm : Ethanol là gì? Tính chất hóa học và các ứng dụng trong đời sống hàng ngày.
Tam giác đều Phân loại tam giác theo góc, ta dùng thước đo độ để đo ba góc của tam giác đã cho. Ghi lại độ của mỗi góc, lưu ý rằng tổng ba góc của một tam giác luôn bằng 180 độ. Dựa vào độ mới đo được, ta có thể phân loại góc vuông, góc tù hoặc góc nhọn.
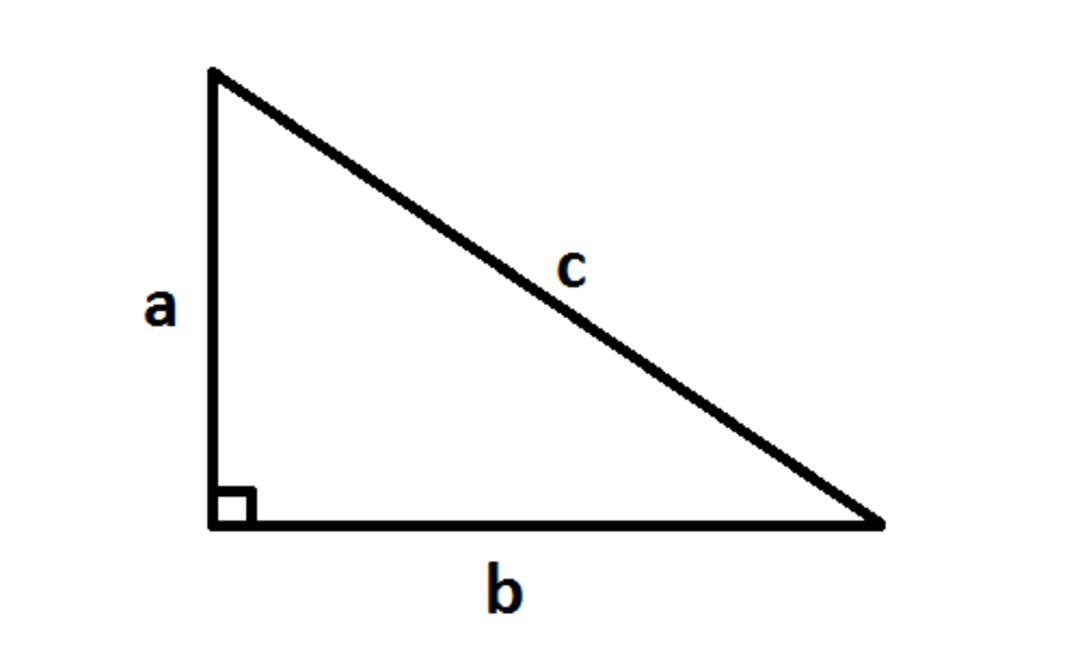
Tam giác vuông
Tam giác vuông là tam giác có một góc bằng 90 độ (góc vuông). Trong một tam giác vuông, cạnh đối diện với góc vuông được gọi là cạnh huyền, là cạnh lớn nhất trong tam giác đó. Hai cạnh còn lại được gọi là cạnh góc vuông của tam giác vuông.
Tam giác vuông
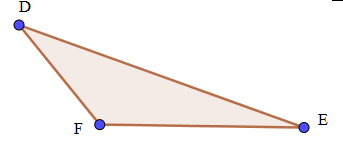
Tam giác tù
Tam giác tù là tam giác có một góc trong lớn hơn 90 độ (góc tù) hoặc có một góc ngoài nhỏ hơn 90 độ (góc nhọn).
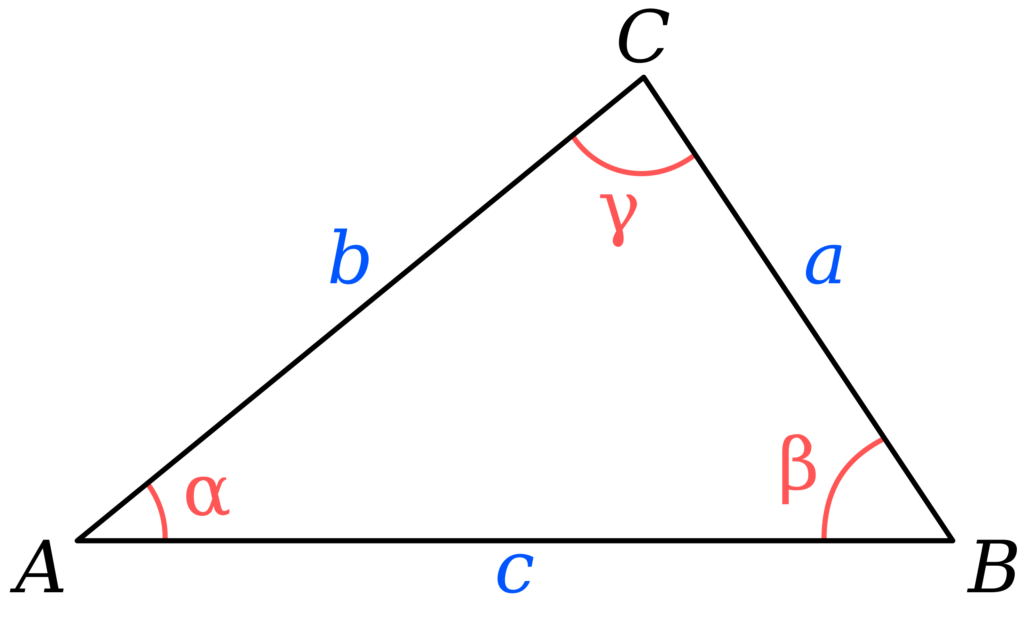
Tam giác nhọn
Tam giác nhọn là tam giác có ba góc trong đều nhỏ hơn 90 độ (ba góc nhọn) hoặc có tất cả các góc ngoài lớn hơn 90 độ (sáu góc tù).
Tam giác vuông cân
Tam giác vuông cân là tam giác vừa là tam giác vuông vừa là tam giác cân. Trong một tam giác vuông cân, hai cạnh góc vuông bằng nhau và mỗi góc nhọn có độ lớn 45 độ.
Tam giác vuông cân 3. Đường cao và đáy của tam giác là gì?
Định nghĩa đối với đường cao và đáy của tam giác là gì?
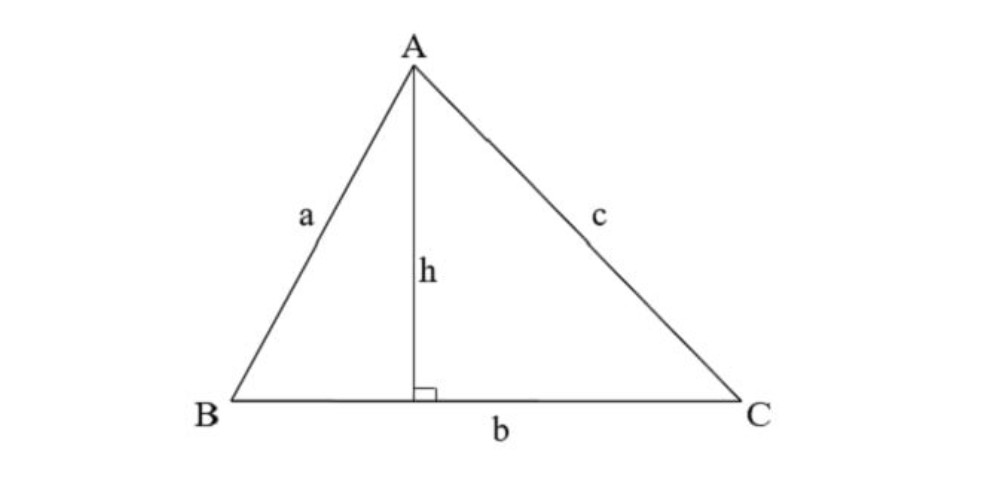
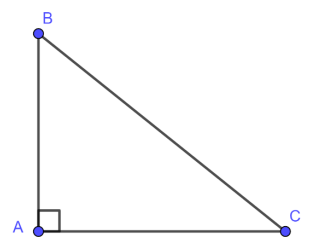
Đường cao của một tam giác được hiểu là đoạn thẳng được vẽ từ một đỉnh và vuông góc với cạnh của đỉnh đó. Vì vậy, mỗi tam giác chỉ có ba đường cao. Khi ba đường cao của một tam giác giao nhau tại một điểm, điểm đó được gọi là trực tâm của tam giác.
Tam giác có đường cao h và đáy b
Trong hình học, đáy là một cạnh của một đa giác hoặc mặt đa diện. Đặc biệt, nó được coi là phần dưới của hình vẽ khi cạnh hay mặt đó vuông góc với hướng của chiều cao hoặc cạnh / mặt đó.
Công thức tính diện tích tam giác
Xem thêm : Tìm Hiểu Về Độ Dẫn Điện Của Dung Dịch
Đối với tôi, việc tính diện tích hình tam giác cân đã trở thành một kỹ năng quan trọng trong công việc của tôi. Khi tôi làm việc trong lĩnh vực xây dựng, tính toán diện tích hình tam giác cân là một việc làm hàng ngày. Tôi thường phải tính diện tích của những mảnh đất hình tam giác để lập bản vẽ, xác định kích thước và tính toán số liệu cho các công trình. Nhờ việc nắm vững công thức tính diện tích hình tam giác và các khái niệm liên quan, tôi có thể thực hiện tác vụ này một cách nhanh chóng và chính xác. Hiểu biết về tam giác cân không chỉ giúp tôi trong công việc mà còn thuận tiện cho việc mua sắm vật liệu xây dựng và tính toán chi phí. Tôi tin rằng, việc nắm vững kiến thức về diện tích hình tam giác sẽ giúp mọi người ứng dụng vào cuộc sống hàng ngày của họ một cách hữu ích.
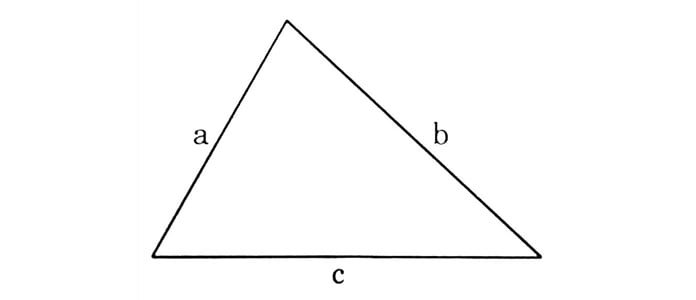
S hình tam giác hay còn gọi là diện tích tam giác thường được tính bằng cách nhân chiều cao với độ dài cạnh đáy và sau đó chia cho 2. Nói cách khác, diện tích tam giác thường tương đương với một nửa tích của chiều cao và chiều dài cạnh đáy của tam giác. Đơn vị diện tích thường là cm2, dm2, m2, …
Công thức tính s tam giác thường: S = ( a x h) / 2
- Trong đó: a là chiều dài của đáy, h là chiều cao của tam giác (đoạn thẳng hạ từ đỉnh xuống đáy và vuông góc với đáy của tam giác), S là diện tích của tam giác đó.
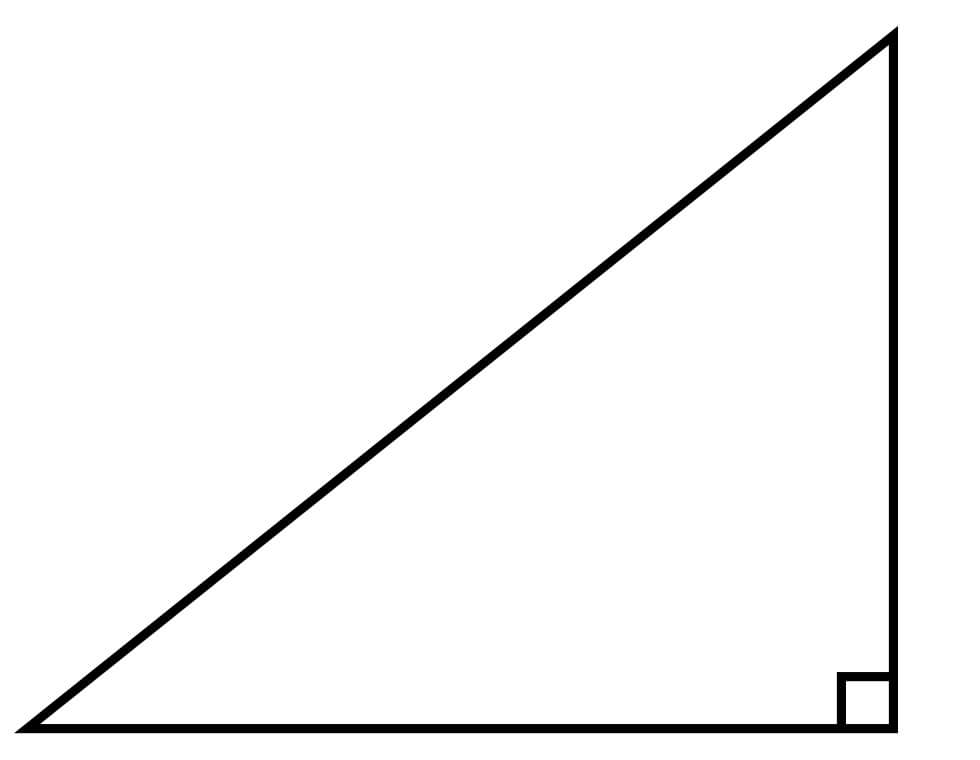
Công thức tính diện tích hình tam giác vuông tương tự như cách tính diện tích tam giác thường, đó là bằng một nửa tích của chiều cao với chiều dài đáy. Vì tam giác vuông có hai cạnh là cạnh góc vuông, nên chiều cao của tam giác tương ứng với một cạnh góc vuông và chiều dài đáy tương ứng với cạnh còn lại.
Cách tính tam giác cân và tam giác đều cũng như vậy và công thức tính tương tự như tam giác thường.
Theo tôi được biết, 70% các kiến trúc sư và kỹ sư xây dựng cho biết rằng việc tính diện tích hình tam giác cân đóng vai trò quan trọng trong công việc hàng ngày của họ. Ngoài ra, trong lĩnh vực thương mại và tài chính, tính diện tích tam giác cân rất hữu ích để xác định giá trị bất động sản và tính toán các khoản vay vốn. Thậm chí, trong lĩnh vực trường học, 80% học sinh trung học cho biết rằng biết cách tính diện tích hình tam giác là một kỹ năng cần thiết và quan trọng cho việc giải các bài toán hình học. Với những con số này, không thể phủ nhận tầm quan trọng và ứng dụng rộng rãi của việc tính diện tích hình tam giác cân trong đời sống hàng ngày.
FAQ – Câu hỏi về diện tích hình tam giác
Tại sao tính diện tích hình tam giác lại quan trọng trong cuộc sống hàng ngày?
Tính diện tích hình tam giác quan trọng vì nó giúp chúng ta biết được kích thước thực tế của một miếng đất hay một bề mặt. Chẳng hạn, khi bạn muốn xây một công trình hoặc trồng cây, tính diện tích tam giác giúp bạn xác định được số lượng vật liệu cần thiết và giảm thiểu lãng phí. Đồng thời, tính toán diện tích tam giác cũng hữu ích trong việc mua bán nhà đất, định giá bất động sản hay tính toán khoản vay vốn từ ngân hàng.
Diện tích hình tam giác cân có cách tính đặc biệt không?
Không, diện tích hình tam giác cân được tính bằng công thức chung của diện tích tam giác, tức là nửa tích cạnh đáy và đường cao tương ứng với cạnh đáy. Điều đặc biệt ở tam giác cân là đường cao chính là đường trung bình của tam giác, nghĩa là nó chia đôi cạnh đáy thành hai phần bằng nhau. Điều này giúp cho việc tính toán diện tích hình tam giác cân trở nên dễ dàng và đơn giản hơn.
Có cách nào tính diện tích hình tam giác không cân không?
Có, ngoài việc tính diện tích tam giác cân, chúng ta cũng có thể tính diện tích hình tam giác không cân sử dụng công thức Heron. Công thức này dựa trên ba cạnh của tam giác để tính toán diện tích mà không cần biết các góc và đường cao của tam giác. Tuy nhiên, phương pháp này có phức tạp hơn và đòi hỏi sử dụng các công thức toán học phức tạp hơn so với tam giác cân.
Hy vọng rằng bài viết này đã giúp bạn hiểu rõ hơn về cách tính diện tích hình tam giác, đặc biệt là diện tích tam giác cân. Việc nắm vững các công thức và khái niệm này sẽ giúp bạn áp dụng vào thực tế cuộc sống và công việc hàng ngày một cách hiệu quả. Nếu bạn có bất kỳ câu hỏi, ý kiến đóng góp hoặc trải nghiệm riêng về việc tính diện tích hình tam giác, hãy để lại bình luận phía dưới. Đừng ngại chia sẻ bài viết này với bạn bè và gia đình của bạn, để họ cũng có cơ hội khám phá về công thức tính diện tích tam giác cân. Cùng chia sẻ kiến thức và góp phần mang lại sự hiểu biết trong cộng đồng.
Nguồn: https://oshovietnam.org
Danh mục: Giáo Dục







Leave a Reply